Computer Graphics (CG) Papers
The Reality of Simulated Actors
Digital Paint Systems: An Anecdotal and Historical Overview
Cameraless Movies, or Humans Wait in the Wings
Infinite Regular Hexagon Sequences on a Triangle
George Lucas Discovers Computer Graphics
The [alpha][delta][gamma]'s of Digital Media Convergence
HWB-A More Intuitive Hue-Based Color Model
Review of The Algorithmic Beauty of Plants
Planar 2-Pass Texture Mapping and Warping
The Video Computer: Image Computing in the Studio
Creating the General-Purpose Image Computer
Plants, Fractals, and Formal Languages
Computer Power for Film and Flight
Special Effects for Star Trek II: The Genesis Demo, Instant Evolution with Computer Graphics
3-D Transformations of Images in Scanline Order
in IEEE Annals of the History of Computing, Oct.-Dec. 2016, vol. 38, no. 4, pp. 74-91.
Abstract. The pixel serves as a unifying concept bringing computer graphics and image processing, indeed all pixel-mediated fields, into a single world called digital light. This article utilizes known instances and original research to reunify the early history of digital light. It shows that the first pictures, video games, and computer animations were in fact created on the earliest computers..
The Reality of Simulated Actors
Communications of the ACM, 36-39, Jul 2001
Abstract. Revisit the topic of the Nov 2000 Scientific American article (see Cameraless Movies below), with tighter predictions and perceptions. The subhead (chosen by the editor) is: The acting of actors will survive the digital revolution; their on-screen appearance may not.
Digital Paint Systems: An Anecdotal and Historical Overview
IEEE Annals of the History of Computing, Vol 23, No 2, Apr-Jun 2001, 4-30 (and cover)
Abstract. This document is based on lectures by the author and Dick Shoup (his article is pp 32-37 of the same issue) on early paint programs at the Computer History Museum in California, Jan 2000. A chronology of pre-1980 digital paint systems is presented, followed by a detailed anecdotal history of some of them, emphasizing the author's experience at Xerox Palo Alto Research Center (PARC) and the New York Institute of Technology (NYIT). See sampling of early paint images, presented in this article. The download below is large (about 40 mb). It includes both my paper and Dick's.
Cameraless Movies, or Digital Humans Wait in the Wings
Scientific American, 72-78, Nov 2000
SUBTITLE (the "deck"): Characters, scenes and entire movies have been crafted digitally. But can animators create realistic digital humans to star in computer-generated films? Actors want to know
ABSTRACT: The completely computer-generated movie is already with us, but is still in the realm of cartoons. When will a "live-action" movie be computer generated? In particular, will human actors be replaced by computer graphic simulations? It is argued that the representations of actors might be replaced but not the acting. In other words, it is valuable to separate the actor from his or her representation, as we do in animation already and as we do on the internet too, when using avatars. The article also estimates, with as much accuracy as can be mustered, when we might expect the representations of humans might reach the point of realism: Not so soon as sometimes predicted.
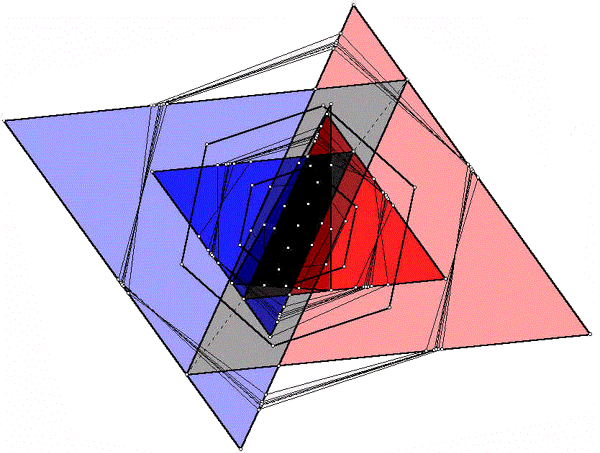
Infinite Regular Hexagon Sequences on a Triangle
Experimental Mathematics, Vol 9, No 3, Nov 2000, 397-406
Abstract. The well-known dual pair of Napoleon equilateral triangles intrinsic to each triangle is extended to infinite sequences of them, shown to be special cases of infinite regular hexagon sequences on each triangle. A set of hexagon-to-hexagon transformations, the hex operators, is defined for this purpose, a set forming an abelian monoid under function composition. The sequences result from arbitrary strings of hex operators applied to a particular truncation of a given triangle to a hexagon. The deep structure of the sequence constructions reveals surprising infinite sequences of non-concentric, symmetric equilateral triangle pairs parallel to one of the sequences of hexagons and provides the most visually striking contribution. Extensive experimentation with a plane geometry educational program inspired all theorems, proofs of which utilize eigenvector analysis of polygons in the complex plane.

©1997-2017, Alvy Ray Smith, All Rights Reserved.
The figure above, from the paper, shows the first two elements of two infinite "sceptre" sequences and two infinite regular hexagon sequences, for any triangle. A sceptre is a pair of congruent equilateral triangles with parallel sides, such that a vertex of each lies on a side of the other - see the figure, where a red-blue pair of equilaterals forms a sceptre. Its name is derived from "symmetric, congruent, equilateral pairs of triangles". The hexagon sequences are centered over the centroid of the given triangle, which is almost obscured by the other forms. (It is almost entirely enclosed by the gray parallelogram.) Notice that the sceptres have sides parallel one of the sequences of hexagons, and their diagonals (dashed line) pass through the centroid of the given triangle. Less obvious: If you join the topmost red triangle vertex to the leftmost blue triangle vertex, the line formed is parallel the other sequence of regular hexagons.
Sketches and scripts for The Geometer's Sketchpad (TGS), illustrating the theorems, are available here. The file hex.txt is a text file explaining the other files available. A Java version of one of the theorems is now online. Try out the theorem interactively.
See other recent geometric art.
A poem, Tools of Vision, by Neelon Crawford, Oct 2000, 35
Friend and expert photographer, Neelon Crawford, is publishing a book of his photographs of "big science" - those superb instruments such as telescopes and accelerators that are used to see the largest and smallest things in our universe. He has asked scientists at the various facilities and his friends to contribute words on the general topic of "tools of vision". My contribution is this poem, my first in print. Tools of Vision is the exhibition catalog for Neelon's photographs on exhibit in the Rotunda Gallery of the National Academy of Sciences, Washington DC, 26 Sep 2000 - 15 Jan 2001. See Polar Fine Arts for photos and writings.
George Lucas Discovers Computer Graphics
IEEE Annals of the History of Computing, Vol 20, No 2: 48-49, 1998
EXCERPT: My colleagues and I have been blessed by a sequence of individuals of a unique variety I call accidental visionaries . . . . Three of them, Alexander Schure (patron of the New York Institute of Technology's computer graphics lab), George (Star Wars) Lucas, and Steven Jobs (cofounder of Apple), have directly influenced my life . . . . This story, for example, is about how filmmaker Lucas discovered computer graphics. (Available electronically, for a fee, from the IEEE Annals 1998 archives. This article is included in a set, called Graphics Remembrances, edited by Jules Bloomenthal.) [Note Rodney Stock's remembrance, immediately following mine, of a key moment in the discovery of the distributed ray-tracing paper that would solve motion blur for Pixar.]
Computer Graphics World, 27-29, Jul 1998
Abstract. On the 25th anniversary of SIGGRAPH, a computer-graphics pioneer reflects on the achievements of the past and the hopes for the future Moore's Law put into more useful form ("10x in 5"). Several dreams that have come true in computer graphics. A list of challenges and non-challenges, the real "to do" list.
The [alpha][delta][gamma]'s of Digital Media Convergence
Proceedings Graphics Interface '98, 51-56, 1998
Abstract. There is no theoretical roadblock obstructing the integration of different media types into a single digital medium—after all, bits are bits—but there are several real problems hindering the so-called digital convergence. The alpha problem is that between premultiplied and non-premultiplied alpha. The gamma problem concerns the nonlinearity that many of today's applications insist on burning into their image data. The delta problem is about the integration of the discrete and the continuous—eg, samples (pixels) and geometry. The subtleties of these are explored—eg, "square pixels" and non-rectangular images—and a current example of how wrong things can get—the US digital television transmission formats battle—is elaborated.
HWB—A More Intuitive Hue-Based Color Model
With Eric Lyons, the journal of graphics tools, Vol 1, No 1: 3-17, 1996
Abstract. The two most common color selector models, other than RGB (Red-Green-Blue), are the hue-based HSV (Hue-Saturation-Value) and HSL (Hue-Saturation-Lightness) color models. It is shown that both of these models are flawed. A closely related model, HWB (Hue-Whiteness-Blackness), is introduced that avoids the flaws, is slightly faster to compute, and is very easy to teach to new users: Choose a hue. Lighten it with white. Darken it with black. That whitening is not the complement of blackening is explained. (The two pages below should be consulted for fixes to errata in the paper.)
C code implementing the color transforms in the paper:
download HWB to RGB transforms
download HSV to RGB transforms
With Jim Blinn, SIGGRAPH 96 Conference Proceedings, Annual Conference Series, 259-268, 1996
Abstract. A classical problem of imaging—the matting problem—is separation of a non-rectangular foreground image from a (usually) rectangular background image-for example, in a film frame, extraction of an actor from a background scene to allow substitution of a different background. Of the several attacks on this difficult and persistent problem, we discuss here only the special case of separating a desired foreground image from a background of a constant, or almost constant, backing color. This backing color has often been blue, so the problem, and its solution, have been called blue screen matting. However, other backing colors, such as yellow or (increasingly) green, have also been used, so we often generalize to constant color matting. The mathematics of constant color matting is presented and proven to be unsolvable as generally practiced. This, of course, flies in the face of the fact that the technique is commonly used in film and video, so we demonstrate constraints on the general problem that lead to solutions, or at least significantly prune the search space of solutions. We shall also demonstrate that an algorithmic solution is possible by allowing the foreground object to be shot against two constant backing colors-in fact, against two completely arbitrary backings so long as they differ everywhere.
Review of The Algorithmic Beauty of Plants
Przemyslaw Prusinkiewicz and Aristid Lindenmayer, Springer-Verlag, New York, 1990, in IEEE Computer Graphics and Applications, Jul 1990, 85-86.
Computer Graphics World, Nov 1988, 90-94. Also, Geometry and Imaging—Two Distinct Kinds of Graphics, Proceedings of the Nippon Computer Graphics Conference (NICOGRAPH 88), Nov 1988, 229-239). Also, Geometry vs Imaging-Extended Abstract, Visualization in Supercomputing, edited by Raul H Mendez, Springer-Verlag, NY, 1990, 151-156. Also, Geometry vs Imaging: Extended Abstract, Geometric Analysis and Computer Graphics, edited by P. Concus, R. Finn, and D. Hoffman, Springer-Verlag, NY, 1991, 169-174.
Planar 2-Pass Texture Mapping and Warping
Computer Graphics, Vol 21, No 4, Jul 1987, 263-272 (SIGGRAPH 87 Conference Proceedings).
Abstract. The 2-pass transformation replaces a 2D (2-dimensional) transformation with a sequence of orthogonal, simpler 1D transformations. It may be used for the closely related processes of texture mapping and warping in computer graphics and image processing. First, texture maps onto planar quadric and superquadric surfaces and, second, planar bicubic and biquadratic warps of images are shown to be 2-pass transformable. A distinction between serial and parallel warps is introduced to solve a confusion in terms between computer graphics and image processing. It is shown that an nth order serial polynomial warp is equivalent to an (n2+n)th order parallel polynomial warp. It is also shown that the serial equivalent of a parallel polynomial warp is generally not a polynomial warp, being more complicated than a polynomial. The ususual problem of bottlenecking and the usual one of anialiasing are discussed in the 2-pass context.
The Video Computer: Image Computing in the Studio
Television Technology: A Look Toward the 21st Century, Society of Motion Picture and Television Engineers, Feb 1987, 23-27 (Selections from the 21st Annual SMPTE Television Conference, San Francisco). Also published in SMPTE Journal, Vol 97, No 3, Mar 1988, 207-208.
Abstract. A general-purpose video computer is proposed which combines many studio or post-production functions, now available only in separate pieces of equipment, and extends their functionality. The ideal machine is described and the current state of the idea is given. The restrictions of realtime and broadcast day are compared. The conclusion is that video computers are already a viable idea within the broadcast-day-turnaround criterion and that the hardware exists as so-called image computers, general-purpose digital computers for the class of computations on images. Consequently software houses could immediately begin preparing applications on video computers for the broadcast video market.
Creating the General-Purpose Image Computer
Computer Graphics World, Jun 1986, pp 63-64.
A description of the Pixar Image Computer, a general-purpose computer for that class of problems dealing with images.
Plants, Fractals, and Formal Languages
Computer Graphics, Vol 18, No 3, Jul 1984, 1-10 (SIGGRAPH 84 Conference Proceedings). Also issued as tutorial notes at SIGGRAPH 84.
Abstract. Although fractal models of natural phenomena have received much attention recently, there are other models of complex natural objects which have been around longer in Computer Imagery but are not widely known. These are procedural models of plants and trees. An interesting class of these models is presented here which handles plant growth, sports an efficient data representation, and has a high "database amplification" factor. It is based on an extension of the well-known formal languages of symbol strings to the lesser-known formal languages of labeled graphs. It is so tempting to describe these plant models as "fractal" that the similarities of this class of models with fractal models are explored in an attempt at rapprochement. The models are not fractal so the common parts of fractal theory and plant theory are abstracted to form a class of objects, the graftals. This class may prove to be of great interest to the future of Computer Imagery. Determinism is shown to provide adequate complexity, whereas randomness is only convenient and often inefficient. Finally, a nonfractal, nongraftal family of trees by Bill Reeves is introduced to emphasize some of the paper's nongrammatical themes.
Computer Power for Film and Flight
Supercomputers, Hearings before the Committee on Science and Technology, U.S. House of Representatives, Ninety-Eighth Congress, No 47, US Government Printing Office, Nov 15-16, 1983, 242-246. Reprinted in Telematics and Informatics, Vol 2, No 4, 1985, 293-398.
Abstract. Recent incorporation of computer graphics into feature-length films -- Return of the Jedi, Star Trek II: The Wrath of Khan, and Tron, to name a few -- has inspired a belief that entire films might soon be generated by computer. It is shown below that even so-called "supercomputers" of today [1983] fall quite short of the power required for this goal. True supercomputers are needed with capabilities just now being conceived and with cost commensurate with typical filmmaking practice. [I predict that a movie will be computed in 1995-2000.]
Some of the most sophisticated and spectacular applications of computer graphics are found in current films.
Abacus, Vol 1, No 1, Fall 1983, 28-45 (Cover story).
A simple tutorial on the use of computer graphics in movies. Inaugural issue of the magazine.
Proceedings of the Nippon Computer Graphics Conference (NICOGRAPH 82), Tokyo, Japan, Nov 1982, 11 pages.
Abstract. The organization of a 3-dimensional computer animation system is described. The basic theoretical foundations of 3D graphics are covered with emphasis on the practical applications. This includes the following topics: antialiasing (sampling and filtering, spatially and temporally), and analytic geometry (splines, polygons, quadrics, and patches). The major subsystems of a typical system are described in some detail: modeling (rigid, articulated, and procedural models), animation (of camera and model), subdivision (hierarchies of primitives, fractals), visible-surface decision (culling, hidden-surface removal, shadows), texture generation (for backgrounds and surfaces), rendering (antialiasing, texturing, shading, bump-mapping), and compositing (matting). The importance of simplified logistics and good human interfaces is emphasized.
Special Effects for Star Trek II: The Genesis Demo, Instant Evolution with Computer Graphics
American Cinematographer, Vol 63, No 10, Oct 1982, 1038-1039, 1048-1050.
Complete details on the creation and production of the Genesis Effect scene in Star Trek II.
Computer Graphics Manual, Jan 1981, 108-112 (Proceedings of ComputerVision 81).
3-D Transformations of Images in Scanline Order
With Ed Catmull, Computer Graphics, Vol 14, No 3, Jul 1980, 279-285 (SIGGRAPH 80 Conference Proceedings). Also issued as tutorial notes at SIGGRAPH 82.
Abstract. Currently texture mapping onto projections of 3D surfaces is time consuming and subject to considerable aliasing errors. Usually the procedure is to perform some inverse mapping from the area of the pixel onto the surface texture. It is difficult to do this correctly. There is an alternate approach where the texture surface is transformed as a 2D image until it conforms to a projection of a polygon placed arbitrarily in 3-space. The great advantage of this approach is that the 2D transformation can be decomposed into two simple transforms, one in horizontal and the other in vertical scanline order. Sophisticated light calculation is also time consuming and difficult to calculate correctly on projected polygons. Instead of calculating the lighting based on the position of the polygon, lights, and eye, the lights and eye can be transformed to a corresponding position for a unit square which we can consider to be a canonical polygon. After this canonical polygon is correctly textured and shaded it can be easily conformed to the projection of the 3D surface.
Computer Graphics, Vol 13, No 2, Aug 1979, 276-283 (SIGGRAPH 79 Conference Proceedings). Also Technical Memo No 6, Computer Graphics Lab, New York Institute of Technology, Jul 1978, issued as tutorial notes at SIGGRAPHs 78, 80-82.
Abstract. To fill a connected area of a digital image is to change the color of all and only those pixels in the area. Fill algorithms for areas defined by sharp boundaries (eg, a white area surrounded by a black curve) have been implemented at several color computer graphics installations. This paper presents an algorithm for the more difficult problem of filling areas with shaded boundaries (eg, a white area surrounded by a curve consisting of several shades of gray). These images may arise from digitizing photographs or line drawings with a scanning video camera, or they may be generated by programs which produce antialiased line segments or dekink black-and-white images. When an area in such an image is to be filled with a new color, it is desirable to have the fill algorithm understand the shaded edges and maintain the shading with shades of the new color instead of the old. The tint fill algorithm presented here accomplishes this task. Its name arises from its ability to change only the tint (hue and saturation) of a pixel, leaving the value (blackness) unchanged. Although the algorithm was motivated by and is written in terms of color, it has a more general interpretation, which is also presented.
Computer Graphics, Vol 12, No 3, Aug 1978, 12-19 (SIGGRAPH 78 Conference Proceedings). Reprinted in Tutorial: Computer Graphics, edited by John C Beatty and Kellogg S Booth, IEEE Computer Society Press, Silver Spring, MD, 2d edition, 1982, 376-383.
Abstract. Digital control of color television monitors -- in particular, via frame buffers -- has added precise control of a large subset of human colorspace to the capabilities of computer graphics. This subset is the gamut of colors spanned by the red, green, and blue (RGB) electron guns exciting their respective phosphors. It is called the RGB monitor gamut. Full-blown color theory is a quite complex subject involving physics, psychology, and physiology, but restriction to the RGB monitor gamut simplifies matters substantially. It is linear, for example, and admits to familiar spatial representations. This paper presents a set of alternative models of the RGB monitor gamut based on the perceptual variables hue (H), saturation (S), and value (V) or brightness (L). Algorithms for transforming between these models are derived. Particular emphasis is placed on an RGB to HSV nontrigonometric pair of transforms which have been used successfully for about four years in frame buffer painting programs. These are fast, accurate, and adequate in many applications. Computationally more difficult transform pairs are sometimes necessary, however. Guidelines for choosing among the models are provided. Psychophysical corrections are described within the context of the definitions established by the NTSC (National Television Standards Committee).
Tutorial: Computer Graphics, edited by John C Beatty and Kellogg S Booth, IEEE Computer Society Press, Silver Spring, MD, 2d edition, 1982, pp 501-515. Also Technical Memo No 7, Computer Graphics Lab, New York Institute of Technology, Jul 1978, issued as tutorial notes at SIGGRAPHs 78-82.
First two paragraphs of the Introduction: Paint is a menu-driven computer program for handpainting 2-dimensional images in full color. It is a highly interactive software package with which a human artist may employ the power of a digital computer to compose paintings that are entirely of his own creation. The "canvas" is actually a large piece of ditigal computer memory that is displayed for the artist on a conventional color television monitor. His "brush" is an electronic stylus resembling an ordinary pen. Its shape can be any 2-dimensional shape he desires, so long as it fits into the canvas memory space. He may choose any color he desires from a "palette" of 256 colors. If this is an inadequate selection, he may mix his own set of colors from a vast set of possibilities.
The main purpose of this tutorial is to describe in detail how an artist accomplishes these acts and what his choices are. In fact, the tutorial is designed to be read as a textbook for Paint users.
This is the paint document on which several patent trials have hinged since it is the first place where RGB painting is recorded, in its Appendix B: Paint3, The RGB Version of Paint. It also records one of the earliest histories in its Appendix C: Brief History of Paint Programs. (Appendix A is a listing of three early equipment configurations used for painting at NYIT.) See also Paint, Table Paint, and Texas as memos that also figured into these litigations.
download the original Paint memo